Данная статья посвящена исследованию методов настройки непрерывных ПИД-регуляторов на примере объектов первого и второго порядка и второго порядка с запаздыванием, а также выбору оптимальной настройки регулятора путем сравнения полученных результатов.
Сразу оговорюсь, что это не статья, а скорее реферат, то есть информация, собранная из разных источников с некой оценкой полезности и эффективности/применимости каждого метода.
Начнем с того, что с настройкой ПИД регулятора можно столкнуться где угодно, например, на преобразователе частоты, и хорошо, если это будет регулятор давления, они настраиваются достаточно просто, если не считать особенностей настройки ПИД, чтобы ПЧ гарантировано "уходил в сон", то есть если отсутствует расход воды, частоник может снизить обороты до указанных минимальных, а дальше просто остановить двигатель и ждать, когда ошибка регулирования не превысит какую-то тоже настроенную величину. В термоконтроллерах чаще всего есть автонастройка, но не всегда она дает приемлемые показатели работы. На сервоприводах контур положения часто тоже имеет ПИ регулятор, он хоть и представляет из себя только часть от ПИД-регулятора, но общие принципы настройки тоже присутствуют, тк имеются основные канал пропорциональный и интегральный.
А что если регулятор не имеет автонастройки и регулируемый объект достаточно сложен, например, чтобы вывести в автонастройку агрегат мощностью 100кВт требуется ее прогрев и работа, а это может составить десятки минут (а иногда и часы, а время- деньги, особенно если это время работы энергоемкого прибора) не говоря уже о себестоимости материала. Тут стоит для начала разобраться в особенностях самого ПИД, чтобы подобрать во-первых подходящий метод, а во-вторых, понять где и как стоит добиваться устойчивости в первую очередь, а где и как можно и потом делать тонкую настройку.
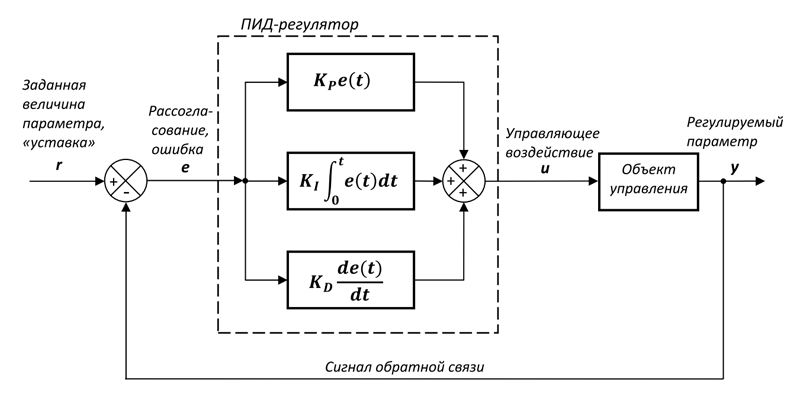
Структура регулятора по классике приведена на картинке, хотя существуют варианты, когда коэффициенты объединяются, это конечно усложняет работу, но общий принцип остается один, главное вовремя заметить, что изменение коэффициента пропорционального влияет например на интегральный канал.
- Пропорциональный канал выдает величину выходного сигнала, который рассчитывается как ошибка (разница, рассогласование) e(t) сигнала обратной связи (ОС) и сигнала задания r, умноженная на коэффициент Kp, который опять же может быть выражен и как 1/Tp - постоянная времени пропорционального канала регулятора. Если убрать (обнулив коэффициенты) остальные составляющий ПИД-регулятора, то результат такого регулятора будет иметь статическую ошибку, тк пропорциональный канал может только компенсировать часть рассогласования. Дальнейшее увеличение значение коэффициента в попытках увеличить эффективность, приведет к перерегулированию (превышению величины над уставкой, иногда многократному и повторяющемуся, в худшем случае в виде автоколебаний) при появлении большого рассогласования (например пуск или резкое изменение параметра). Данный канал отвечает за быстродействие регулятора в целом и наибольшую часть работы (компенсация большей части рассогласования).
- Интегральный канал в общем тоже берет за основу ошибку регулирования, но при этом выход интегрирует эту ошибку, умноженную на коэффициент Ki (1/Ti). Это дает возможность компенсации статической ошибки, если система не испытывает внешних возмущений (со временем конечно, если процесс не устойчивый, это событие может и не наступить), но не избавляет от динамической. Попытки уменьшить динамическую ошибку или как-то уменьшить время, за которое регулятор компенсирует ошибку, приведут к тому, что тоже появится перерегулирование и почти гарантировано автоколебания (ну как минимум несколько затухающих даже на фоне отсутствия перерегулирования в целом, если пропорциональный канал имеет слабое значение).
- Дифференциальный канал подает на выход скорость изменения ошибки de/dt, умноженную на коэффициент Kd (1/Td), что дает возможность как бы предугадать описанное выше резкое изменение рассогласования (пуск или резкое изменение параметра) и тем самым помочь своим более медленным братьям компенсировать величину ошибки. В дальнейшем, когда вступят в дело каналы пропорциональный и интегральный, роль дифференциального канала должна затухать. Конечно отыграют и электрические составляющие, и задержка расчета, и механика с инерцией, которая часто является самой долгой в перечне задержек, но что-то все же можно получить и от этого канала. Дифференциальный канал чувствителен к ВЧ-помехам. Поэтому, при построении системы регулирования, необходимо принять меры для защиты от помех. Кстати в теории дифференциальный канал может уменьшить значение перерегулирования, полученного при настройки пропорционального и интегрального канала за счет более быстрого уменьшения ошибки регулирования до вмешательства других каналов.
Итак теперь перейдем непосредственно к методам настройки
Ручная настройка или метод настройки "по графикам".
Часто можно услышать о простейшем подходе к настройке (сейчас говорим о ручной), когда вручную настраивают сперва Kp, предварительно обнулив остальные каналы, потом Ki, а последним Kd, оценивая результат работы чисто по графикам процессе (так называемый эмпирический и эвристический методы), либо пользуясь ТАУ (нахождение частоты устойчивости и отступ от нее на 2-4 лога), такая инструкция встречается практически для всех ПЧ и даже сервоприводов, возможно это оправдано тем, что процесс быстрый и графики можно получить без особых затрат просто перебирая коэффициенты по логарифмической шкале, но для температуры так будет настраивать неудобно. Да-да если коэффициент равный двум слишком мал, а введение в коэффициент цифры 4 не дало необходимого изменения, нет смысла вводить K=6, нужно вводить 8, а потом 16, смысл в том, что мы тем самым ищем нужную нам частоту среза, а она как многие помнят из ТАУ у нас на логарифмической шкале выложена, и если она далеко, то перебор по обычной шкале сильно удлинит время поиска.
Важное замечание: даже для одного и того же объекта процедуру настройки ПИД регулятора следует повторять, если изменились параметры объекта (например, загрузка печи) или значительно изменилась рабочая температура (остывание и соответственно отток мощности зависит от градиента температур).
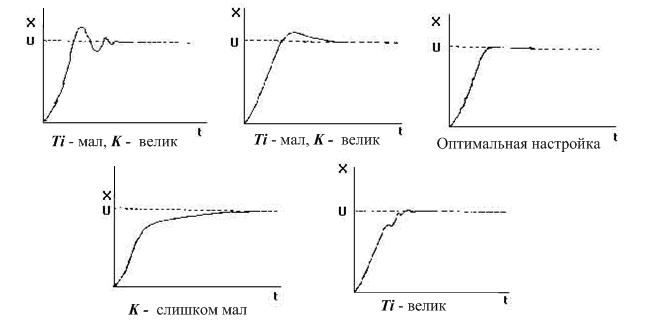
Второй вариант больше подходит для долгих процессов (температура) - предварительно нужно вывести систему на границу устойчивости. Для этого нужно вывести регуляторы И и Д (записать нули), оставив только П (пропорциональный), устойчивость необходимо проверять на той температуре, которая близка к рабочей, то есть эксперименты с большим Кр нужно проводить уже после выхода на установившийся процесс, до этого лучше постараться выбрать коэффициент поменьше, либо уменьшить его уже когда перескочили уставку. На установившемся процессе добиваемся увеличением Кп коэффициента появления заметных колебаний, либо если колебания уже есть, то уменьшаем Кр до их исчезновения, полученный коэффициент Кркр запомним. Что делать с полученной частотой среза (частота, на которой настройка теряет устойчивость)? Переведем ее в период колебаний τ (хотя можно сразу измерить именно период колебаний τ). Далее для термоконтроллеров Термодат предлагает следующую таблицу.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 2*Кркр | Выключено | Выключено |
| P+I | 2.2*Кркр | 0.8* τ | Выключено |
| P+I+D | 1.7*Кркр | 0.5*τ | 0.12*τ |
Для других применений думаю лучше пользоваться методом "по графикам" для ручной настройки.
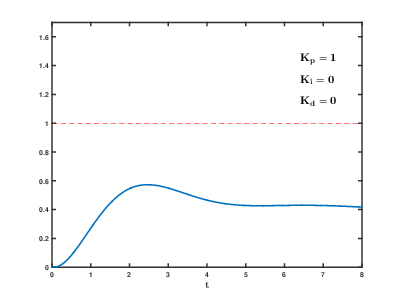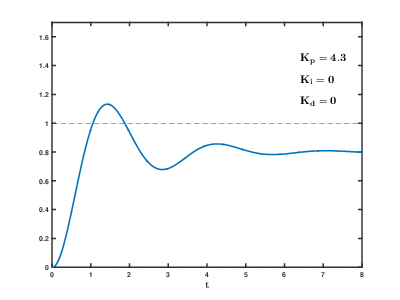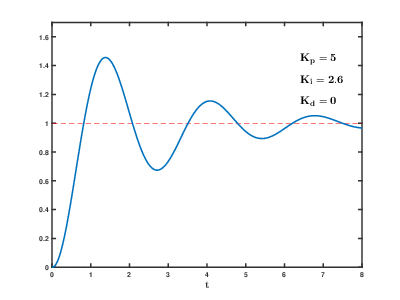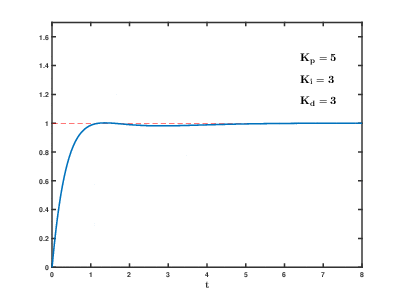
Тангенциальный метод настройки ПИД-регулятора (первый метод Зиглера-Никольса).
Следующий метод, который предлагается опять же для настройки ПИД регулировки температуры, это Тангенциальный метод.
В тангенциальном методе для нахождения ПИД коэффициентов используется переходная характеристика объекта, в случае терморегулирования кривая разогрева объекта.
Для начала опишу метод, который предлагается производителем приборов Термодат (коэффициенты соответственно могут отличаться у разных производителей).
В режиме ручного управления контроллера задается некоторое значение мощности на нагрузке. Значение мощности должно быть таким, чтобы установившаяся температура не превысила допустимого значения. Нужно дождаться установления температуры Т1, в этом режиме и в некоторый момент времени скачком изменить значение мощности (например: на 5%). Записать процесс изменения температуры (на компьютере, на самописце или по точкам, вручную) до установления нового устоявшегося значения температуры Т2.
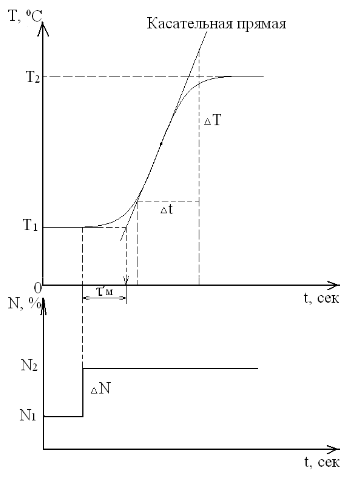
Провести касательную к полученной кривой в точке, где наклон касательной будет максимален.
Определить «мёртвое» время процесса как промежуток времени, прошедший с момента изменения мощности до момента времени, определяемого точкой пересечения касательной и средней линии температуры первого устойчивого состояния Т1 (до изменения мощности нагрева).
Определить величину относительного наклона касательной по формуле:
К = (∆T/∆t)/∆N.
∆T - изменение температуры в °С,
∆t - соответствующее изменение времени в секундах,
∆N - изменение мощности в %.
Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 100*τм*К | Выключено | Выключено |
| P+I | 111*τм*К | 3.3*τм | Выключено |
| P+I+D | 83*τм*К | 2*τм | 0.25*τм |
К сожалению данный метод имеет еще пару трактовок, посему приведу обе, а решать какая лучше подойдет вам. Оба используют только два параметра для описания объекта, проводится линия по участку, соответствующему максимальному наклону графика переходной характеристики.
Первый вариант основан на поиске мертвого времени и длительности переходного процесса.
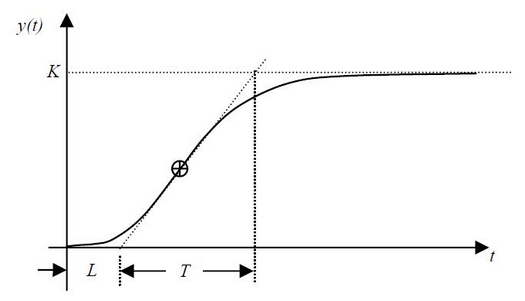
В первом случае ищется пересечение с осью времени и с мнимой линией максимального задания, значения параметров L и T, используются в расчете, формулы приведены в таблице:
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti=Kp/Ki |
Дифференциальный коэффициент Td=Kd/Kp |
| Только P | T/L | Выключено | Выключено |
| P+I | 0.9*T/L | L/0.3 | Выключено |
| P+I+D | 1.2*T/L | 2*L | 0.5*L |
Второй вариант использует: a и L, которые определяются по графику переходной характеристике объекта управления так:
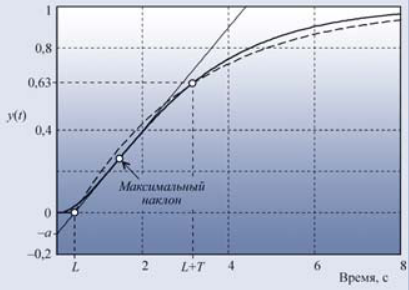
Формулы для расчета коэффициентов сведены в следующую таблицу:
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
| Только P | 1/a | Выключено | Выключено |
| P+I | 0,9/a | 3*L/Kp | Выключено |
| P+I+D | 1,2/a | 0,9*L/Kp | 0.5*L/Kp |
Замечание: метод Зиглера-Никольса даёт параметры, далёкие от оптимальных. Это объясняется не только упрощённостью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом, исходя из требования к декременту затухания, равному 4, что и даёт медленное затухание процесса колебаний.
Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод даёт слишком малый запас устойчивости. Но все же для начальной настройки вполне пойдет.
Метод колебаний (или второй частотный метод Зиглера-Никольса)
Данный метод основан на поиске частоты устойчивости, на которой сдвиг по фазе в разомкнутом контуре равен 180°.
Назначить уставку Тус, равной температуре регулирования (или 0.7Тус, если перегрев во время настройки нежелателен, а он может быть значительным).
Тоже существует два варианта, первый упрощенный от Термодата:
Включить позиционный (пороговый) режим регулирования.
В установившемся режиме колебаний температуры измерить период τ колебаний температуры (время между соседними максимальными или минимальными значениями температуры). Измерить также полный размах колебаний температуры ΔТ=Тmax-Тmin (разность максимального и минимального значений температуры).
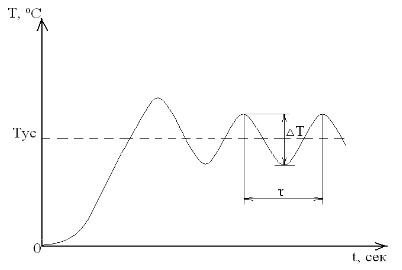
Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей. Параметр «Ограничение ПИД» или «Зона» (если он есть в приборе) сделать равным Kp.
| Тип регулирования | Пропорциональный коэффициент Kp |
Интегральный коэффициент Ki |
Дифференциальный коэффициент Kd |
| Только P | 1.4*∆Т | Выключено | Выключено |
| P+I | 1.6*∆Т | 2.4*τ | Выключено |
| P+I+D | 1.2*∆Т | 1.5*τ | 0.2*τ |
Второй вариант такой:
Настройка пропорциональной компоненты (Kp)
1.Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются (Kи =0, Kд = 0) и задаем некоторое целевое значение регулируемого параметра (например, температуры):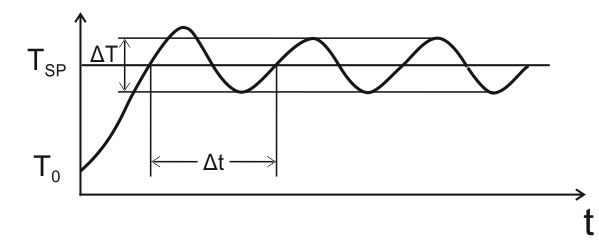
Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры (в расчетах не участвует);
∆t — период колебаний температуры.
2.Меняем значение пропорциональной составляющей Kp от минимума (можно от 0) до момента, пока не появятся устойчивые колебания системы с периодом ∆t. Фиксируем это значение как Kуст, а также период колебаний системы ∆t. Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, колебания должны быть одинаковы относительно Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ∆t – полный период. Данное время есть характеристика системы, оборудования.
3.На этом практическая часть метода заканчивается. Из полученных значений рассчитываем коэффициенты ПИД:
Kp=0.6⋅Kуст
Ki=(2⋅Kp)/∆t
Kd=(Kp⋅∆t)/8
Здесь Kуст – тот самый коэффициент пропорциональной составляющей, при котором возникли колебания, а ∆t – период этих колебаний.
Второй вариант, когда надо найти постоянные времени Ti и Td
Используя полученные параметры рассчитываем Ти и Тд по таблице.
| Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
|
| П-регулятор | 0.5*Kуст | ||
| ПИ-регулятор | 0.4*Kуст | 0.8*∆t/Kp | |
| ПИД-регулятор | 0.6*Kуст | 0.5*∆t/Kp | 0.125*∆t/Kp |
Хочется сказать, что данный метод не несет за собой никаких улучшений, просто он построен на другом способе поиска, недостатки те же, что и у метода Зиглера-Никольса первого.
Метод CHR (Chien, Hrones и Reswick) или Чина-Хронеса-Ресвика, если по-русски
Этот метод предполагает предварительное определение времени задержки L и времени выравнивания T по переходной характеристике объекта. Ну это мы делали и для Зиглера-Никольса, но в отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20 процентного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера-Никольса. Метод CHR даёт две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (таблица), вторая – при наблюдении отклика на внешние возмущения (не представлена). Какую систему параметров выбирать, зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки или ослабление внешних воздействий (в жизни изменение уставки вызывает намного более существенные процессы в регулятора, потому лучше настраивать по этой таблице, будет настройка не "в малом", а "в большом"). Если же важно и то и другое, то необходимо использовать регуляторы с двумя степенями свободы. Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой. В CHR используются те же исходные параметры a и L, что и в методе Зиглера-Никольса. Обратим внимание, что пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.
Формулы для определения коэффициентов приведены в таблице:
| Без перерегулирования | С 20% перерегулированием | |||||
| Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
Пропорциональный коэффициент Kp |
Интегральный коэффициент Ti |
Дифференциальный коэффициент Td |
|
| П-регулятор | 0.3/a | 0.7/a | ||||
| ПИ-регулятор | 0.35/a | 1.2*L/Kp | 0.6/a | L/Kp | ||
| ПИД-регулятор | 0.6/a | L/Kp | 0.5*L/Kp | 0.95/a | 1.4*L/Kp | 0.47*L/Kp |
Остальные методы, а именно Спектральный метод, метод Куна, метод Стогестада, метод Шеделя требуют уже больших знаний ТАУ и самое главное требуют либо реальной переходной характеристики, которую придется искать методом интерполяции и аппроксимации, либо вовсе моделирования объекта управления. Если вкратце, то суть методов можно описать парой предложений.
Спектральный метод
Спектральный метод предполагает компенсацию нулями регулятора нежелательных полюсов объекта.
На основе полюсов объекта {p1, p2} определяются компенсирующие значения постоянных времени интегрального и дифференцирующего каналов:
Tи = |1/p1|, Tд = |1/p2|.
и коэффициенты регулятора Kp и Kd в виде:
Kp = Ki(Tи + Tд), Kd = Ki*Tи*Tд/(Tи + Tд).
Метод Куна
Параметром, характеризующим быстродействие любых рассматриваемых объектов, является суммарная постоянная времени. Метод настройки Куна (или метод «Т-правило») основан на аппроксимации объекта звеном третьего порядка. Параметры ПИД-регулятора Ti и Td выбирают, таким образом, чтобы компенсировать два полюса. Расчетные значения для регулятора даны в таблице, но я здесь ее приводить не стану.
Метод Стогестада
По идентифицированным параметрам модели ОУ находят необходимые параметры настройки регулятора. Принцип синтеза ПИД-регулятора с использованием метода Стогестада заключается в следующем: задание желаемого вида переходной характеристики замкнутой САУ (желаемый вид описывается инерционным звеном первого порядка) путем выбора постоянной времени.
Для апериодического звена второго порядка с транспортным запаздыванием параметры ПИД-регулятора могут быть найдены по следующим формулам:
kp = T1/k*(Tc+τ), Ti=min[T1;c(Tc+τ)],Td=T2.
где T1, T2, k и τ–параметры объекта; с–параметр, который рекомендуют принимать равным 4, для обеспечения апериодического вида переходного процесса на выходе системы управления (например пароперегревателем котла).
Метод Шеделя
Метод Шеделя основан на принципе каскадного коэффициента демпфирования. В методе обобщается понятие коэффициента демпфирования на случай системы 3-го порядка. Параметры ПИД-регулятора должны быть выбраны таким образом, чтобы коэффициенты демпфирования системы принимали определенные значения. Их если будет интересно лучше поискать в справочниках.



